
Python求均值 方差 标准差 Jak的博客 Csdn博客 Python求方差
补充知识:python —— rolling()std() #在这里我们取天内的标准差 以上这篇基于python计算滚动方差(标准差)talib和pdrolling函数差异详解就是小编分享给大家的全部内容了,希望能给大家一个参考。三、实现一个总体方差的置信区间 (1 ) 样本均值为21, 样本标准差为2, 样本量为50; ( 2) 样本均值为13, 样本标准差为002 , 样本量为15; ( 3 ) 样本均值为167, 样本标准差为31, 样本量为22; Question1 根据以上样本结果,计算总体方差的90 % 的置信区间?
Python 标准差公式
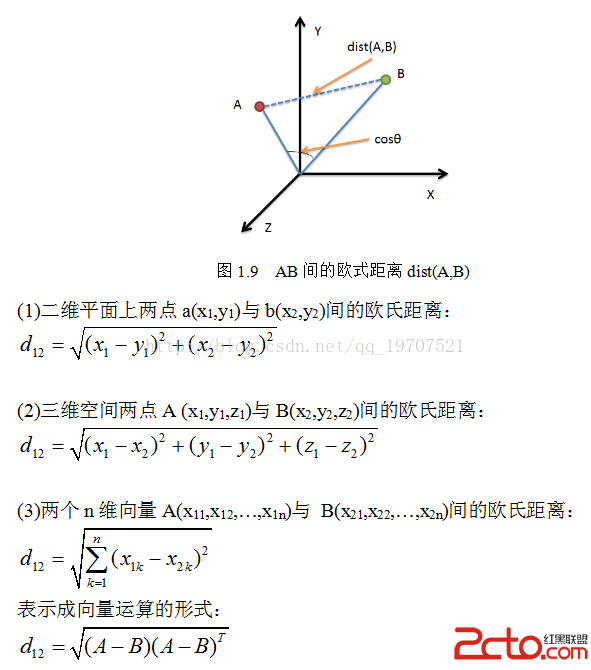
Python 标准差公式- 自定义标准差标准化函数 def StandardScaler (data) data= (datadatamean ())/datastd () return data ##对菜品订单表售价和销量做标准化 data4=StandardScaler (detail 'counts') data5=StandardScaler (detail 'amounts') data6=pdconcat ( data4,data5,axis=1) print ('标准差标准化之前销量和售价数据为:\n', 标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差 经过简单的推导就可以得到两个n维向量a(x11,x12,,x1n)与 b(x21,x22,,x2n)间的标准化欧氏距离的公式: Python实现辛普森

推断统计分析 一 Python验证正态分布 大数定理 中值极限定理 墨天轮
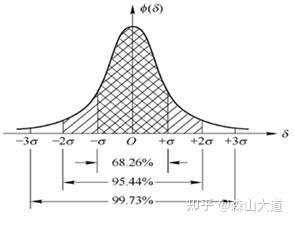
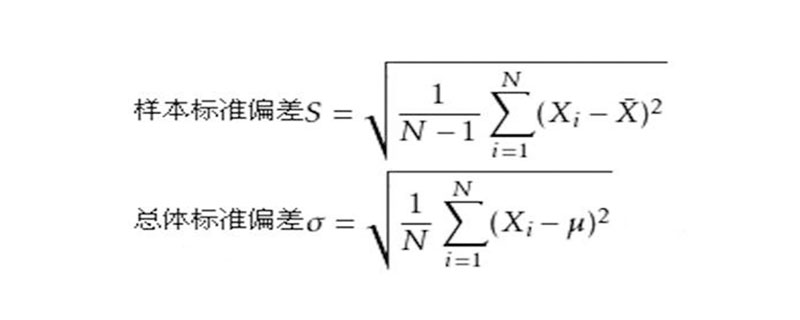
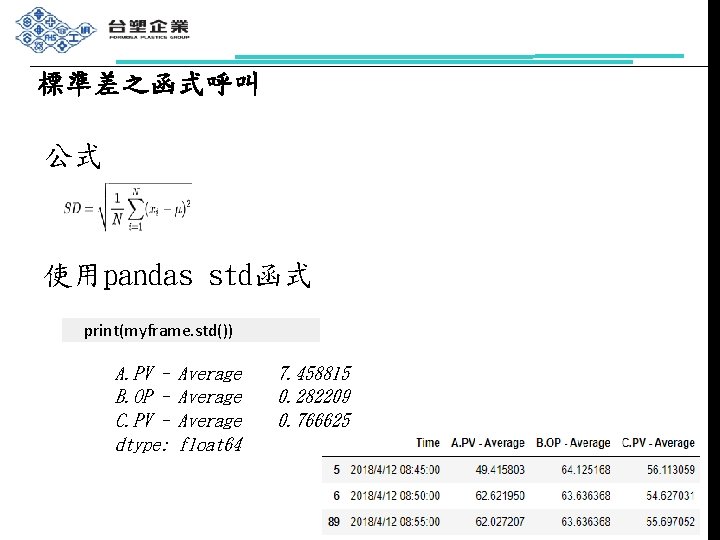
Var (X) = E (XEX)^2 称为 X (或分布 F )的方差,其平方根 \sqrt {Var (X)} 称为 X (或分布 F )的标准差 方差和标准差是刻画随机变量在其中心位置附近散布程度的数字特征。 注意:样本方差和总体方差的区别 统计学上对于样本方差的无偏估计使用如下公式计算: s^2 = \frac {1} {n1} \sum\limits_ {i=1}^n (x_i \bar {x})^2 前面有一个系数 \frac {1} {n1} ,当时当样本数量很大的时候, e=npmean (d) 5/6 e的二次开方,就是矩阵a的标准差,又叫做均方差。 e**05 6/6 numpy把上述求标准差的过程,包装成函数std。 npstd (a) 与求平均值的方法一致,还可以按行求标准差、按列求标准差。 编辑于,内容仅供参考并受版权保护 直接上代码 #调出numpy import numpy as np arr = 2, 4, 6, 8, 10, 12 # 要计算的数值 # 求均值 arr_mean = npmean(arr) # 求方差 arr_var = npvar(arr) # 求标准差 arr_std = npstd(arr, ddof=1) # 数值输出 print("平均值为:%f" % arr_mean) print("方差为:%f" % arr_var) print("标准差
Pandas计算标准差 标准差(或方差),分为总体标准差(方差)和样本标准差(方差)。 前者分母为n,后者为n1。后者是无偏的。 pandas里的dfstd()和dfvar()都是算的无偏的。 而numpy是有偏的。 如果需要用pandas的std()方法计算有偏标准差,可以用下面两种方法: 计算偏度和峰度 def calc_stat(data) niu, sigma, niu3=calc (data) n= len (data) niu4= 00 # niu4计算峰度计算公式的分子 for a in data a = niu niu4 = a** 4 niu4 /= n skew = (niu3 3 *niu*sigma** 2 niu** 3 )/ (sigma** 3) # 偏度计算公式 kurt=niu4/ (sigma** 4) # 峰度计算公式下方为方差的平方即为标准差 pythonnumpystd()计算矩阵标准差 1 >>> a = nparray(1, 2, 3, 4 ) 2 >>> npstd(a) # 计算全局标准差 3 4 >>> npstd(a, axis=0) # axis=0计算每一列
Python 标准差公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
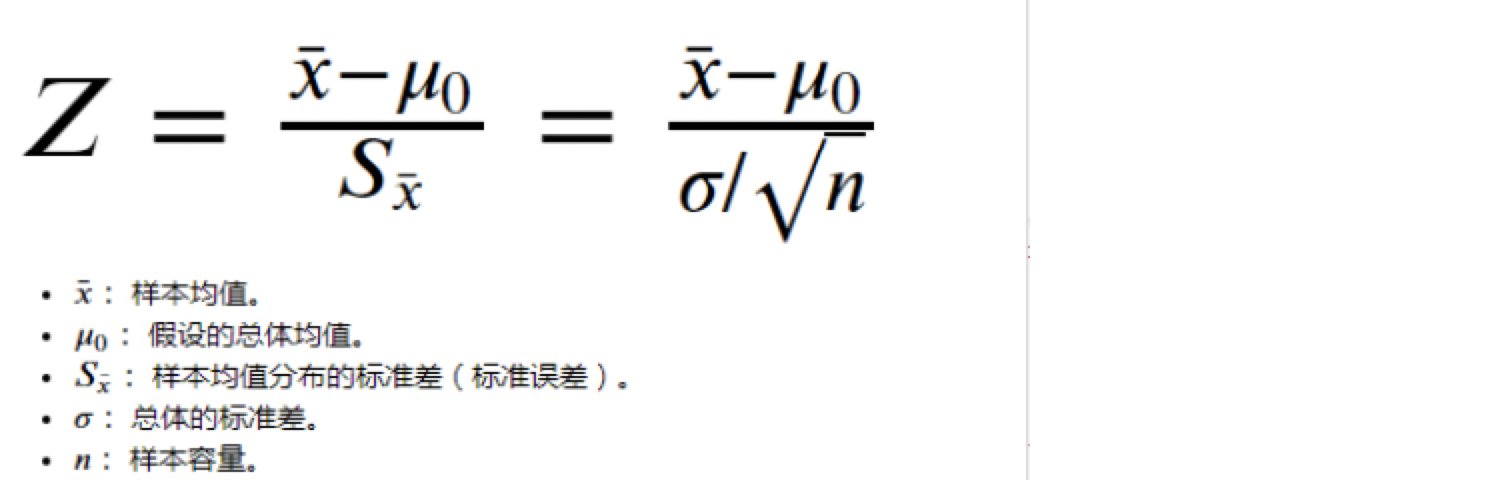 |  |  |
 |  |  |
 |  |  |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
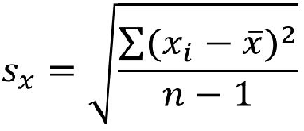 |  |  |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 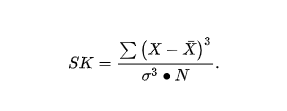 |  |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 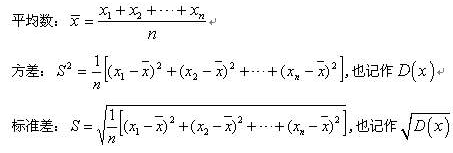 | |
 |  |  |
 |  | 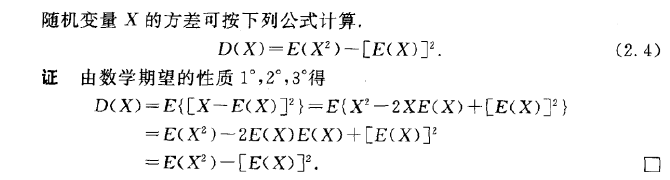 |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
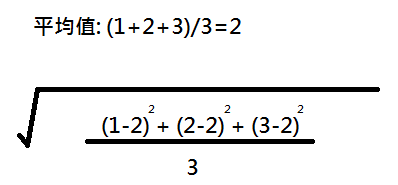 |  | |
 |  | |
 |  | |
「Python 标准差公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 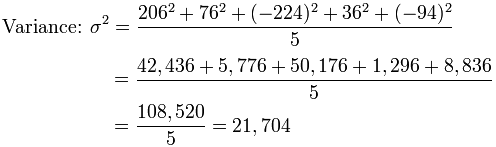 |
样本标准偏差的方差=((125)^2 (225)^2 (325)^2 (425)^2)/3 = ()/4 = 5/3 所以对5/3开方运算所得到的就是样本标准偏差为:129 同样适用numpy的std函数就可以做到这点,只需要将其一个Optional的参数设定为1即可,代码&执行如下: 那么在 ZScore 标准下,A 的成绩会比 B 的成绩好。 我们能看到 ZScore 的优点是算法简单,不受数据量级影响,结果易于比较。不足在于,它需要数据整体的平均值和方差,而且结果没有实际意义,只是用于比较。 在python中使用如下:





0 件のコメント:
コメントを投稿